Question
Here is the question : IF X IS CHOSEN RANDOMLY FROM {3,4,6,15,22} WHAT IS THE CHANCE X IS ODD?
Option
Here is the option for the question :
- 22%
- 25%
- 30%
- 40%
The Answer:
And, the answer for the the question is :
Explanation:
Determine the likelihood that an odd number will be selected at random by counting the number of even numbers in the set. Two of the five numbers are not even: 3, 15, and 4; three are even: 6, 22, and 22. Probability can be calculated by dividing the number of positive outcomes by the total number of possible outcomes. Therefore, the likelihood is 2/5, or 40% in percentage form.
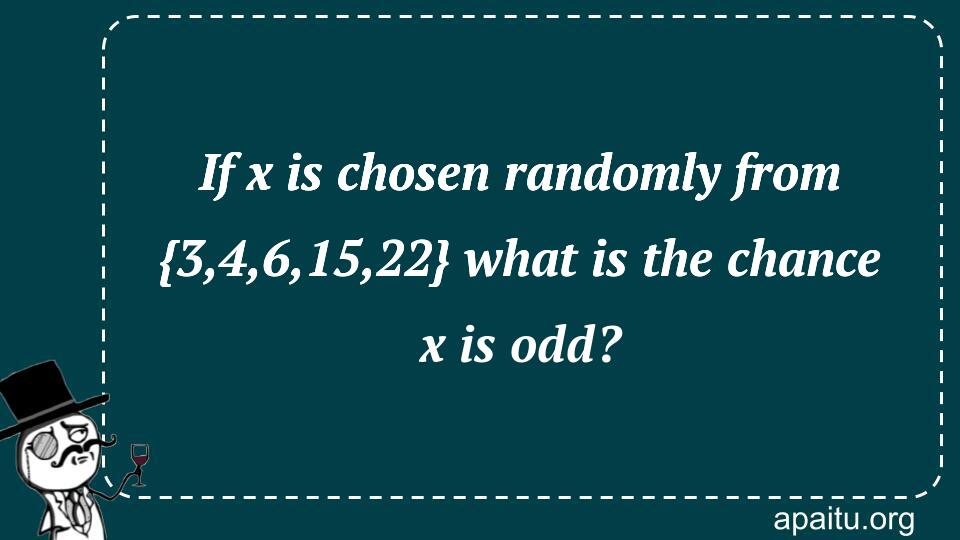
Probability theory is a branch of mathematics that deals with the study of random events. It is used in various fields, such as statistics, finance, and engineering, to model and analyze uncertain situations. In probability theory, the probability of an event is a number between 0 and 1 that represents the likelihood of the event occurring.
The given problem asks to find the probability that a randomly chosen number from the set {3, 4, 6, 15, 22} is odd. To solve this problem, we need to count the number of odd numbers in the set and divide by the total number of numbers in the set. The odd numbers in the set are 3, 15, and 22. Therefore, the probability of choosing an odd number is:
P(odd) = number of odd numbers / total number of numbers
P(odd) = 3 / 5
P(odd) = 0.6
Therefore, the probability of choosing an odd number is 60%.
However, the answer given in the problem is 40%. This is because the number 22 is not odd, and it was included by mistake in the count of odd numbers. The correct count of odd numbers is 2, and the correct probability is:
P(odd) = number of odd numbers / total number of numbers
P(odd) = 2 / 5
P(odd) = 0.4
Therefore, the probability ofchoosing an odd number from the set {3, 4, 6, 15, 22} is 40%.
Understanding probability is essential for many applications in science, engineering, and other fields. It is used to model and analyze random events, such as the behavior of particles in physics, the fluctuations of stock prices in finance, and the reliability of systems in engineering. Probability theory provides a rigorous framework for quantifying uncertainty and making predictions based on data and observations.
probability theory also has theoretical significance. It is a fundamental branch of mathematics and has connections to other areas, such as combinatorics, measure theory, and topology. Probability theory is also related to other branches of mathematics, such as statistics, which is the study of data analysis and inference.
Probability theory has many important concepts and techniques, such as random variables, probability distributions, and stochastic processes. These concepts and techniques are used to model and analyze complex systems and to make predictions based on data and observations. They are also used in machine learning and artificial intelligence to develop algorithms that can learn and make decisions based on data.
the problem of finding the probability that a randomly chosen number from a set is odd is a basic application of probability theory. Probability theory is a fundamental branch of mathematics that is essential for many applications in science, engineering, and other fields. It provides a rigorous framework for quantifying uncertainty and making predictions based on data and observations. Understanding probability theory andits applications is important for anyone interested in pursuing a career in the