Grade 8: If -3(j + 7) = -9, what is j?

Question

Here is the question : GRADE 8: IF -3(J + 7) = -9, WHAT IS J?

Option

Here is the option for the question :

• 21
• 6
• -4
• -10

The Answer:

And, the answer for the the question is :

Explanation:

In the eighth grade, pupils are required to solve for a letter, often requiring negative values, which makes introductory algebra more challenging.

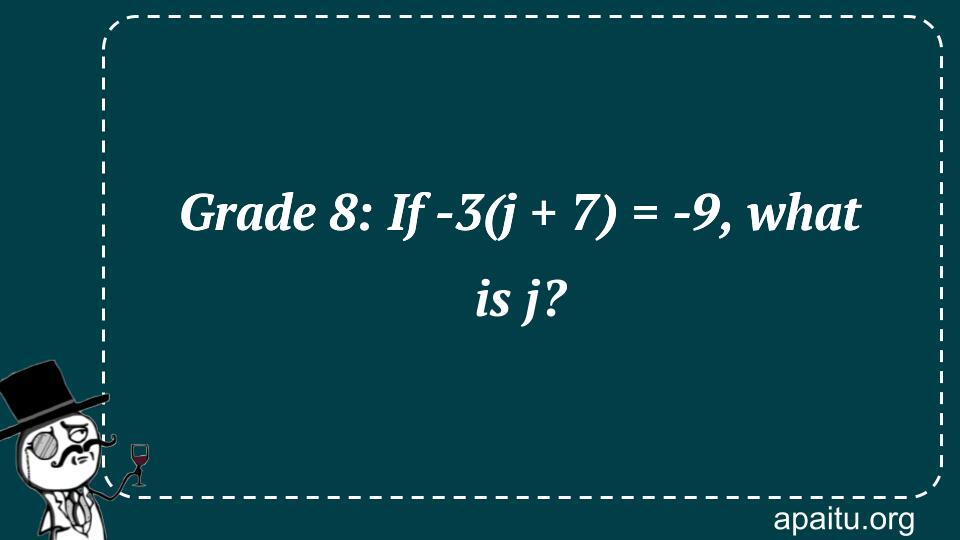
In Grade 8 mathematics, students delve into the world of equations and learn to solve for unknown variables. Equations are mathematical statements that express the equality between two quantities. By applying various operations and solving for the unknown variable, we can determine its value. Let’s explore an example involving the solution of an equation: finding the value of j in the equation -3(j + 7) = -9. By simplifying and solving the equation step by step, we find that the value of j is -4.

In this problem, we are given the equation -3(j + 7) = -9, and we are asked to find the value of j.

To solve this equation, we follow these steps:

Distribute the -3 to the terms inside the parentheses: -3j – 21 = -9.

Simplify the equation by combining like terms: -3j – 21 + 21 = -9 + 21, which becomes -3j = 12.

Divide both sides of the equation by -3 to isolate the variable j: (-3j)/(-3) = 12/(-3), resulting in j = -4.

Hence, the value of j in the equation -3(j + 7) = -9 is determined to be -4.

Understanding how to solve equations is crucial as it allows us to find the values of unknown variables and establish relationships between different quantities. Grade 8 students who develop a solid understanding of solving equations lay the foundation for more advanced algebraic concepts, problem-solving strategies, and mathematical reasoning.

Equations are encountered in various real-life situations. They are used in science, engineering, finance, and many other fields to model and solve problems. By mastering the skill of solving equations, students develop the ability to analyze and solve real-world problems, make logical deductions, and communicate mathematical solutions effectively.

Furthermore, understanding equations enhances students’ critical thinking and problem-solving skills. It enables them to analyze complex situations, break them down into manageable parts, and apply mathematical techniques to find solutions. By studying equations, students also gain a deeper understanding of the interconnectedness of mathematical concepts and the power of logical reasoning.

students will encounter more complex equations and systems of equations as they progress in their mathematical education. These advanced concepts further expand students’ mathematical toolkit and equip them with valuable problem-solving skills for a wide range of applications.

in Grade 8 mathematics, solving equations is a fundamental skill. By applying various operations and isolating the variable, we can determine its value. In the case of the equation -3(j + 7) = -9, the value of j is found to be -4. Mastering the skill of solving equations not only improves mathematical proficiency but also enhances students’ problem-solving abilities and logical reasoning, enabling them to tackle more complex mathematical challenges in the future.