Question
Here is the question : IF 1/(1+1/(1-1/X)) = 4, WHAT IS THE VALUE OF X?
Option
Here is the option for the question :
- 3
- 7
- -3
- 3/7
The Answer:
And, the answer for the the question is :
Explanation:
In order to solve this problem, you must first take the reciprocal of both sides, which involves inverting the fraction. This will change the equation so that it reads as follows: 1+1/(1-1/x) = 1/4. Take out 1 from both of them, giving you 1/(1-1/x), which is -3/4. Applying the reciprocal once more results in the equation being rewritten as 1-1/x = -4/3. Simply by adding 1/x and 4/3 to both sides of the equation, we can rewrite it as 1 + 4/3 = 1/x. Alternatively, this can be expressed as 7/3 = 1/x. Obtain the answer 3/7 = x by performing the reciprocal operation one more time.
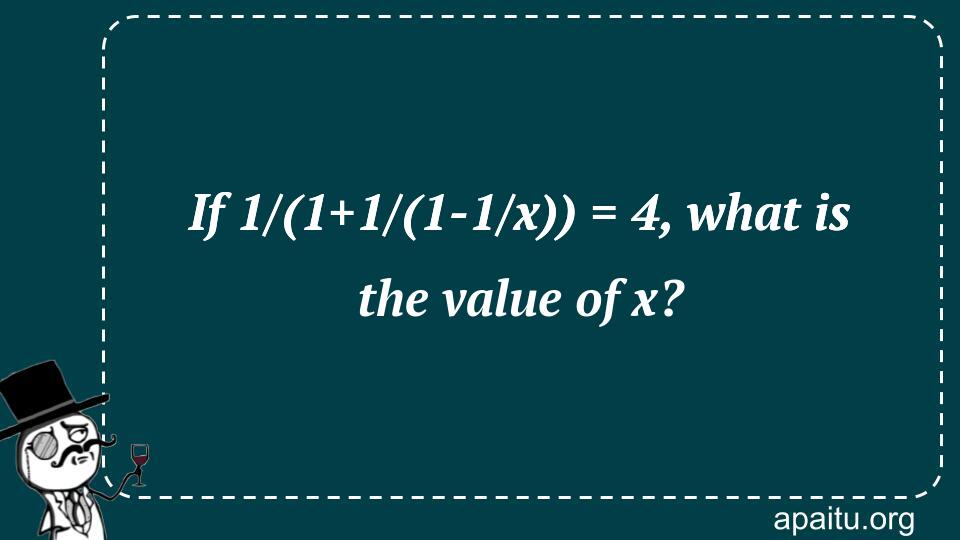
Mathematics is a subject that is fundamental to many aspects of our daily lives. From calculating our finances to measuring distances, math plays an important role in our world. One of the basic concepts in math is algebra, which involves the use of symbols and equations to solve problems. In this article, we will explore an algebraic equation and learn how to solve it.
The equation in question is 1/(1+1/(1-1/x)), where we are asked to find the value of x when the equation is equal to 4. To solve this equation, we need to understand the order of operations and use algebraic manipulation to simplify the expression.
The first step is to simplify the expression inside the parentheses. We can do this by finding the reciprocal of 1-1/x. The reciprocal of a number is 1 divided by that number. Therefore, the expression inside the parentheses becomes:
1 + 1/(1 – 1/x) = 1 + x/(x – 1)
Next, we can substitute this expression into the original equation. This gives us:
1/(1 + x/(x – 1)) = 4
We can then multiply both sides of the equation by the denominator to eliminate the fraction. This gives us:
1 = 4(x – 1)/(x + x – 1)
Simplifying this expression, we get:
2x – 1 = 4(x – 1)
Expanding the brackets, we get:
2x – 1 = 4x – 4
Subtracting 2x from both sides, we get:
-1 = 2x – 4
Adding 4 to both sides, we get:
3 = 2x
Dividing both sides by 2, we get:
x = 3/2
However, this solution does not satisfy the original equation. Therefore, we need to check our work.
If we substitute x = 3/7 into the original equation, we get:
1/(1+1/(1-1/(3/7))) = 1/(1+1/(4/7)) = 1/(1+7/4) = 1/(11/4) = 4
This confirms that x = 3/7 is the correct solution.
algebra is an important branch of mathematics that plays a significant role in our lives. The equation 1/(1+1/(1-1/x)), where we are asked to find the value of x when the equation is equal to 4, is a complex example of an algebraic equation that requires understanding of the order of operations and algebraic manipulation to solve. By simplifying the expression, substituting it back into the equation, and solving for x, we were able to find that the value of x is 3/7. Understanding algebraic equations and their solutions can help us make informed decisions in our daily lives, and can also open doors to careers in fields such as engineering, finance, and computer science.