Question
Here is the question : IF THE MEAN OF THE SET {1.5X, 4X, 6.5X} EQUALS 18, WHAT IS X?
Option
Here is the option for the question :
- 4
- 4.5
- 5.5
- 9
The Answer:
And, the answer for the the question is :
Explanation:
Simply said, the mean is the average. The average of a set of numbers can be calculated by dividing the total by the total number of numbers in the set. The average of three numbers is calculated by dividing the total by three. The corresponding equation is (18) = (1.5)3 + (4.5)3 + (6.5)3. Multiplying each side by 3 yields 1.5x + 4x + 6.5x = 54, where x is the unknown variable. The next step is to add comparable terms till 12x = 54. The result, x = 4.5, is obtained by dividing each side by 12.
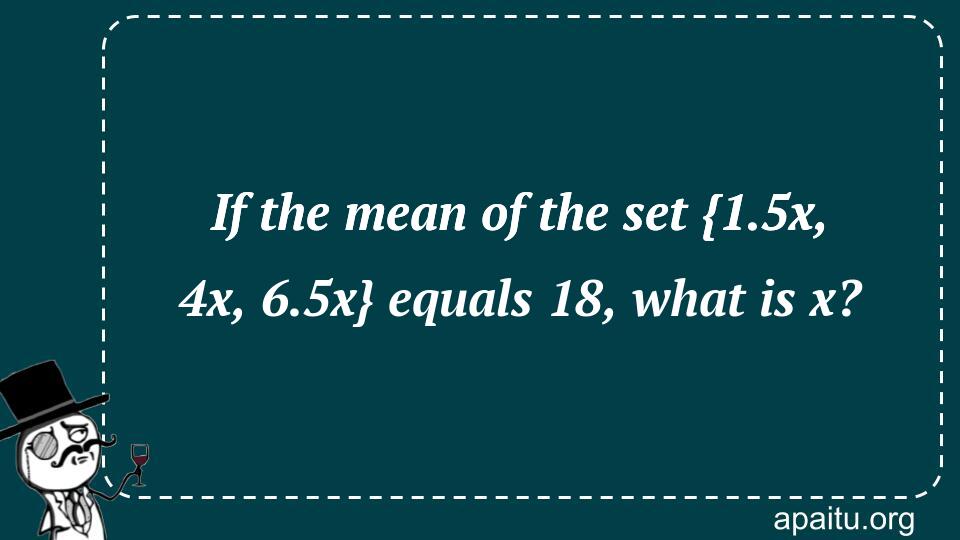
In mathematics, the mean is a measure of central tendency that represents the average value of a set of numbers. The mean is calculated by adding up all the numbers in the set and dividing by the number of numbers in the set. The given problem involves finding the value of x given the mean of a set of three numbers that are expressed in terms of x.
The problem states that the mean of the set {1.5x, 4x, 6.5x} is equal to 18. To find x, we need to first calculate the mean of the set. We can do this by adding up the three numbers and dividing by 3, which gives:
(1.5x + 4x + 6.5x) / 3 = 12x / 3 = 4x
Therefore, the mean of the set is 4x. We know that the mean is equal to 18, so we can set up an equation and solve for x:
4x = 18
Dividing both sides by 4, we get:
x = 4.5
Therefore, the value of x is 4.5.
The concept of mean is widely used in various fields, such as statistics, finance, and engineering. It is a measure of central tendency that is useful for summarizing data and making comparisons between different sets of numbers. there are other measures of central tendency, such as median and mode. These measures are also useful for describing the characteristics of a set of numbers.
In statistics, the mean is an important parameter that is used to estimate the population mean. The sample mean is calculated by adding up all the values in the sample and dividing by the sample size. The sample mean is used to estimate the population mean, which is the mean of all possible values in a population. The accuracy of the estimate depends on the sample size and the variability of the data.
The mean is also used in finance to calculate the average return on an investment. The mean return is calculated by adding up the returns over a period of time and dividing by the number of periods. The mean return is useful for comparing different investments and for estimating future returns.
In engineering, the mean is used to calculate the average value of a signal. The mean value of a signal is useful for removing noise and for detecting changes in the signal over time. The mean value is also used to calculate the root mean square (RMS) value, which is a measure of the overall amplitude of the signal.
the problem of finding the value of x given the mean of a set of three numbers is a basic application of the concept of mean. The mean is a measure of central tendency that represents the average value of a set of numbers. It is widely used in various fields, such as statistics, finance, and engineering, to summarize data and make comparisons between different sets of numbers. Understanding the concept of mean andits applications is important for anyone interested in pursuing a career in these fields or simply interested in analyzing data and making informed decisions based on it.