Question
Here is the question : IF X + 2 = 27, AND 2X + 7 = Z, WHAT IS THE VALUE OF Z?
Option
Here is the option for the question :
- 3
- 39
- 57
- 92
The Answer:
And, the answer for the the question is :
Explanation:
This requires two algebraic steps to solve. To begin, we can solve the initial problem by subtracting 2 from either side of x + 2 = 27 to get x = 25. Now, enter 25 into x in the second equation. The formula should read 2(25) + 7=z. The following step appears to be 50 + 7 = z, which leads to the conclusion that z = 57 due to the precedence of multiplication over addition in the order of operations.
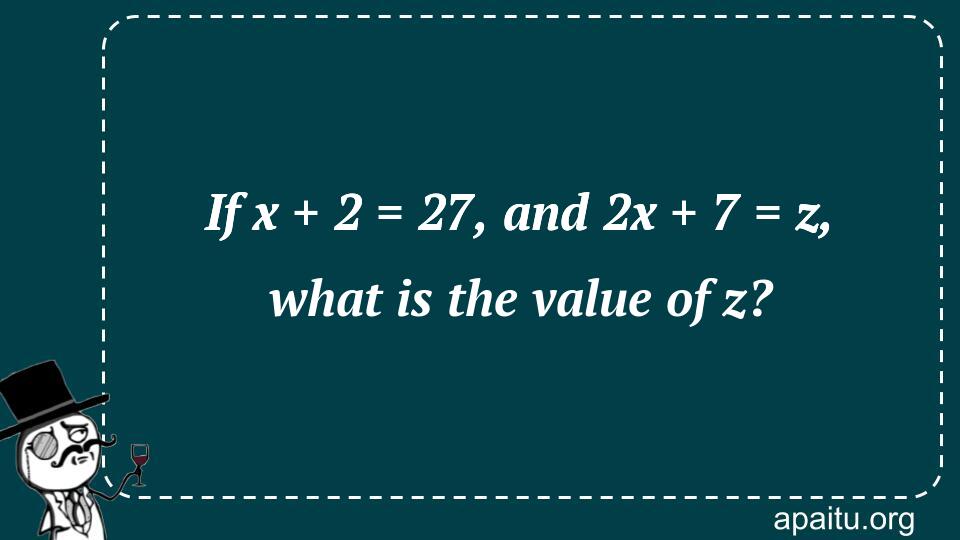
In mathematics, solving equations is a fundamental skill that is essential for many applications in science, engineering, and other fields. One common type of equation is the linear equation, which involves one or more variables raised to the first power.
The given problem involves two linear equations with two variables: x and z. The first equation is x + 2 = 27, which can be solved by subtracting 2 from both sides of the equation, yielding x = 25. The second equation is 2x + 7 = z. To solve for z, we substitute the value of x from the first equation into the second equation, giving:
2(25) + 7 = z
Simplifying the expression on the left-hand side, we get:
50 + 7 = z
Combining like terms, we get:
57 = z
Therefore, the value of z is 57.
The process of solving equations is not just about finding the correct answer, but also about understanding the underlying concepts and principles. Linear equations, in particular, are important because they are fundamental to many areas of mathematics and science. They are used to model relationships between variables, such as in physics, where they can be used to describe the motion of objects under different conditions.
linear equations also have theoretical importance. They are the building blocks of more complex equations and systems of equations, which are used to model a wide range of phenomena. Linear equations can besolved using a variety of methods, including substitution, elimination, and graphing. These methods are based on the properties of equations and the rules of algebra, such as the distributive property, the addition and subtraction property of equality, and the multiplication and division property of equality.
Solving equations also requires attention to detail and careful manipulation of symbols and numbers. It is important to keep track of operations, such as adding, subtracting, multiplying, and dividing, and to use the correct order of operations. Errors in solving equations can lead to incorrect results and can have serious consequences in real-world applications.
the problem of solving linear equations is an important and fundamental skill in mathematics and science. The given problem involving two linear equations with two variables demonstrates the process of solving equations, which involves substituting values, simplifying expressions, and applying algebraic rules. The solution, z = 57, provides the value of the second variable given the values of the first variable and the coefficients of the equations. Linear equations are essential for modeling relationships between variables and for solving a wide range of problems in various fields.