Question
Here is the question : “IF X = Y, AND Y = 7, THEN X MUST EQUAL 7” IS AN EXAMPLE OF WHAT PROPERTY?
Option
Here is the option for the question :
- Transitive property of equality
- Substitution property of equality
- Division property of equality
- Reflexive property of equality
The Answer:
And, the answer for the the question is :
Explanation:
One of the properties of equality in mathematics is called the transitive property. If a = b and b = c, then a = c, is the generic formula for this property. Many geometry formulas, including those involving congruent angles, triangles, and circles, can be solved with the help of this characteristic. The features of equality that are commonly used in mathematics are substitution (if x = y and x = z, then y = z), symmetry (if x = y then y = x), and reflexivity (if x = x).
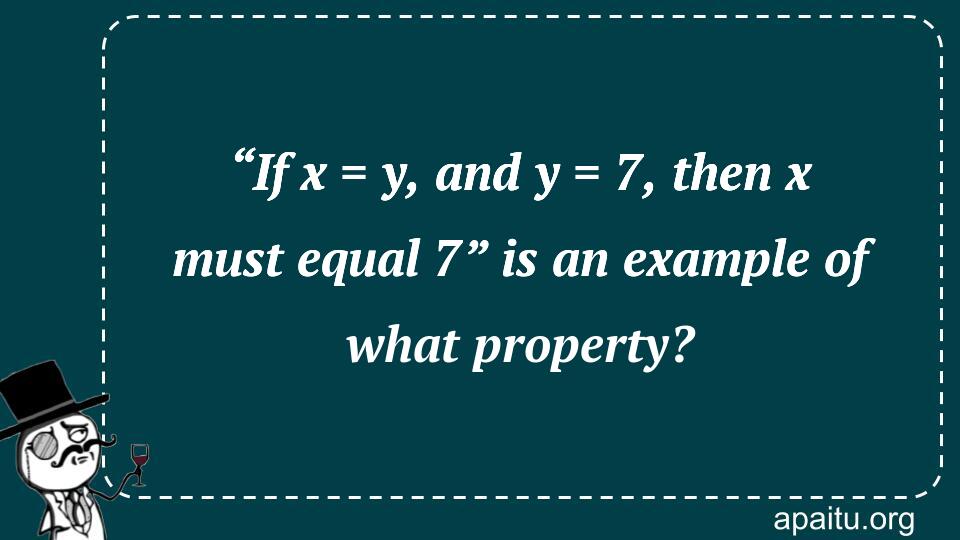
The transitive property of equality is a fundamental concept in mathematics that states that if a equals b and b equals c, then a equals c. In other words, if two things are equal to a third thing, then they are equal to each other. The example given, “If x = y, and y = 7, then x must equal 7,” is an example of the transitive property of equality in action.
The transitive property of equality is one of the basic properties of equality in mathematics. It allows us to make logical connections between different equations and statements, and to simplify complex expressions by substituting equivalent values.
For example, if we know that a equals b and b equals c, we can substitute b for a and c for b in any equation or expression, and the result will still be true. This allows us to simplify expressions and solve equations more easily.
The transitive property of equality is used in many areas of mathematics, including algebra, geometry, and calculus. It is also used in many real-world applications, such as engineering, physics, and computer science.
Understanding the transitive property of equality is important for solving many types of mathematical problems. It allows us to reason logically about equations and expressions, and to make connections between different mathematical concepts.
there are several other fundamental properties of equality in mathematics, including the reflexive property, the symmetric property, and the substitution property.
The reflexive property states thatany number or variable is equal to itself, such as a = a. The symmetric property states that if a equals b, then b equals a, such as if x = 5, then 5 = x. The substitution property states that if a equals b, then b can be substituted for a in any equation or expression.
All of these properties of equality are important for understanding and solving mathematical problems. They allow us to reason logically about equations and expressions, and to simplify complex problems by substituting equivalent values.
the transitive property of equality is a fundamental concept in mathematics that allows us to make logical connections between different equations and statements. It is used in many areas of mathematics and real-world applications, and is essential for solving many types of mathematical problems. Understanding the transitive property of equality, along with the other properties of equality, is important for developing strong mathematical skills and problem-solving abilities.